Implicit Differentiation Questions

Find ${dy\over dx}$ when $x$ and $y$ satisfy:

$e^{xy} = e^{4y} - e^{5x}$
$\cos(xy)=\sin(x-y)$
$y\tan(x+y) = 4$
$e^{\cos(x)} + e^{\sin(y)} = {1\over 4}$
$e^{xy} + \ln(xy) = \text{cosec}(x) + 4$

Solutions We apply the derivative operator ${d\over dx}$ to each equation and rearrange to get ${dy\over dx} = \dots$. The step-by-step solutions for 1. is provided, and the final solutions to the others only being provided.

The left-hand side is equal to \[{d\over dx}e^{xy} = e^{xy}\cdot {d\over dx}(xy) = e^{xy}(y+ x{dy\over dx}) = ye^{xy} + xe^{xy} {dy\over dx}.\] And the right-hand side is equal to \[{d \over dx}(e^{4y} - e^{5x}) = e^{4y}{d\over dx}(4y) - e^{5x}{d\over dx}(5x) = 4e^{4y}{dy\over dx} - 5e^{5x}.\] So we have that: \[ ye^{xy} + xe^{xy}{dy\over dx} = 4e^{4y}{dy\over dx} - 5e^{5x} \] which rearranges to: \[ xe^{xy}{dy\over dx} - 4e^{4y}{dy\over dx} = -ye^{xy} -5 e^{5x}. \] So we have that \[ (xe^{xy} - 4e^{4y}) {dy\over dx} = -ye^{xy} - 5e^{5x} \] and finally so: \[ {dy\over dx} = \frac{-ye^{xy} - 5e^{5x}}{xe^{xy} - 4e^{4y}} = \frac{ye^{xy} + 5e^{5x}}{ 4e^{4y}- xe^{xy}} \]
\[ {dy\over dx} = \frac{\cos(x-y) + y\sin(xy)}{\cos(x-y) - x\sin(xy)} \]
\[ {dy\over dx} =\frac{-y\sec^2(x+y)}{\tan(x+y) +y\sec^2(x+y)} \]
\[{dy\over dx} = \frac{\sin(x)e^{\cos(x)}}{\cos(y)e^{\sin(y)}}\]
\[{dy\over dx} = -1 - \frac{xy \text{cosec}(x)\cot(x)}{xye^{xy} + 1}\]

Find all the points $(x,y)$ on the graph $(x^2+y^2)^2 = 2x^2 - 2y^2$ where $y’ = 0$.

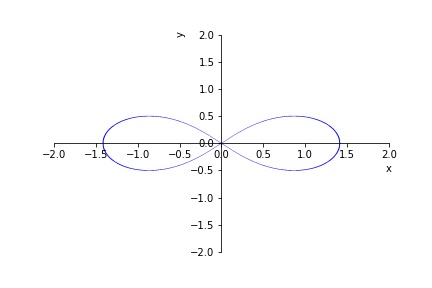
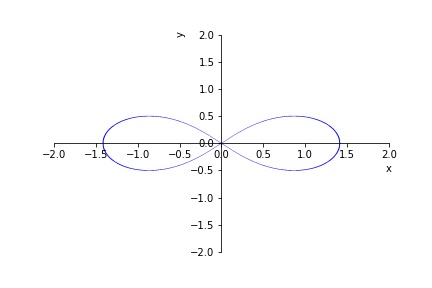
Step 1: Find an expression for ${dy\over dx}$ by taking the $x$ derivative of the equation: \[\begin{align} {d\over dx} (x^2+y^2)^2 &= {d\over dx}(2x^2- 2y^2) \\ 2(x^2 + y^2) {d\over dx}(x^2+y^2)&=4x - 4y {dy\over dx} \\ 2(x^2 + y^2)(2x +2y{dy\over dx})&=4x - 4y {dy\over dx} \\ 4y(x^2 + y^2){dy\over dx}+ 4y{dy\over dx}&=4x-4x(x^2 + y^2)\\ {dy\over dx}&= {x(1-(x^2 + y^2))\over y(1+(x^2 + y^2))} \end{align}\]
Step 2: Solve ${dy\over dx}=0$. This can occur when $x = 0$ and $y\neq 0$, so let’s investigate possible solutions of this type. Substituting this into the equation for the curve, we have that $y^4 = -2y^2$, which if $y\neq 0$, leaves $y^2 =-2$, which has no real solutions. So we are left with the requirement that $1-(x^2 + y^2)=0$. So we have that the equation of the curve becomes $1 = 2x^2 - 2y^2$. We can eliminate either $x$ or $y$ using the equation $1 = x^2 + y^2$ - I will choose to eliminate $x^2$. Then we have that $x^2 = 1-y^2$. So \[1=2x^2 -2y^2 = 2(1-y^2)-2y^2 = 2-4y^2.\] So we have that $4y^2 = 1$, which gives us solutions of $y = \pm {1\over 2}$. Thus we have that \[x^2 = 1-(\pm {1\over 2})^2 = 1-{1\over 4} = {3\over 4}.\] Giving $x = \pm {\sqrt{3}\over 2}$. So the final solutions are: \[(x,y) = ({\sqrt{3}\over 2},{1\over 2}), \ (-{\sqrt{3}\over 2},{1\over 2}),\ ({\sqrt{3}\over 2},-{1\over 2}),\ (-{\sqrt{3}\over 2},-{1\over 2}) \]

Find the equation of the tangent line to the curve: $y^2 e^{2x}=3y + x^2$ at the point $(0,3)$

Step 1: Find an expression for ${dy\over dx}$ in terms of $x$ and $y$. We do this by taking the $x$-derivative of the equation of the curve: \[ \begin{align} {d\over dx}(y^2 e^{2x}) &= {d\over dx}(3y + x^2)\\ 2y{dy\over dx}e^{2x} + 2y^2e^{2x}&=3{dy\over dx} + 2x. \end{align} \] After rearranging we have that \[ \begin{align} (2ye^{2x} - 3){dy\over dx} &= 2x - 2y^2 e^{2x}\\ {dy\over dx}&= \frac{2x - 2y^2 e^{2x}}{(2ye^{2x} - 3)}. \end{align} \] Thus we have that ${dy\over dx}$ at the point $(x,y) = (0,3)$ is equal to ${dy\over dx} = -{18\over 3} = -6$. So the tangent line would have equation $y = -6x + c$, and intersects the original curve at the point $(0,3)$, thus $3 = -6\cdot 0 + c \implies c = 3$. Thus the tangent line has equation $y = -6x +3$.

Show that ${dy\over dx}$ for the curve given by $(x+y)(x^2 - xy + y^2)=1$ is:

\[ {dy\over dx} = - {x^2 \over y^2} \] whenever $y\neq 0$

Find the equation of the normal when $x=0$.

To simplify the calculation we expand the brackets to get that \[ \begin{align} (x+y)(x^2-xy+y^2) &= x^3 - x^2y + xy^2 + yx^2 - xy^2 + y^3 \\ &= x^3 + y^2. \end{align} \] So the equation is just $x^3 + y^3 = 1$, we then take the $x$ derivative to give: \[ {d\over dx}(x^3 + y^3) = 3x^2 + 3y^2 {dy\over dx} = 0, \] which rearranges to the answer.
At $x=0$, we have that $y^3 = 1$, which has real solution $y=1$, so the tangent line at $(x,y)=(0,1)$ is given by $y = 0\cdot x + c$ as ${dy\over dx} = -\frac{0}{1} = 0$ at $(x,y)=(0,1)$. Thus the tangent line is a constant line $y = 1$. The normal equationIf this is confusing to you, think about the graph $y=1$ and then construct a perpendicular line that goes through the point $(0,1)$

is therefore just $x=0$.

Find the points $(x,y)$ on the graph $x^{2/3} + y^{2/3} =8$, where $y’ = 1$.

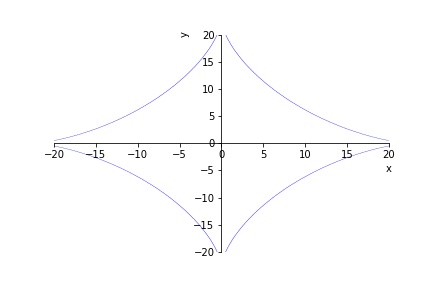
Taking the $x$ derivative of the equation we have that: \[ {2\over 3}x^{-1/3} + {2\over 3}y^{-1 /3}{dy\over dx} = 0. \] Which rearranges to: \[ {dy\over dx} = - {x^{-1/3}\over y^{-1/3}} = - \frac{y^{1/3}}{x^{1/3}}. \] This equals $1$, when $y^{1 /3} = - x^{1/3}$, and by cubing this equation we have that $y = - x$. So we need to simultaneously satisfy the equations $x^{2/3} + y^{2/3} =8$ and $y = -x$. Notice that $(-x)^{2/3} = ((-x)^{1/3})^2 = ((-1)^{1/3}x^{1/3})^2$, assuming we are only interested in the realThere are also complex numbers which are the cube root of -1, but we will ignore those

solutions to this equation we have that $(-1)^2 x^{2/3}=x^{2/3}$. So we have that $2x^{2/3} = 8$, thus $x^2= 4^{3} = 64$ and thus $x=\pm 8$. So the points of the graph are $(x,y) = (8,-8),\ (-8,8)$.

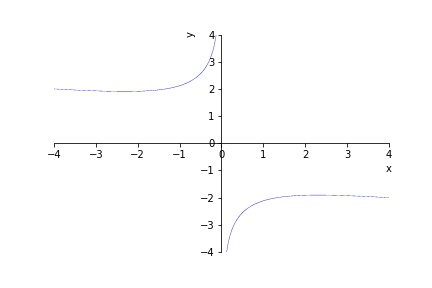
The curve C is described by the equation $3x^2 + 2xy^3 + 16 = 0$. Show that the normal to C at the point $x=-4$ is parallel to the normal to C at $x=4$.
Find the distance between the y-intercepts of these two normals.

When $x=+ 4$ the equation simplifies to $y^3= -8$, with $y=-2$ its solution. And when $x=-4$, we have that $y^3 = 8$ and thus $y=2$.

The normal line to these points are then found by first finding the tangent line. To do this we need an expression for the gradient, $dy \over dx$, which we get by taking the $x$-derivative of the equation: \[\begin{align} 6x + 2y^3 + 6xy{dy\over dx} = 0\\ {dy\over dx} = {-3x -y^3 \over 3xy} \end{align} \]

Thus the gradient at $(x,y) = (4,-2)$ is equal to \[{dy \over dx} = {-12 + 8 \over -24 }=-{4\over 24} = - {1\over 6}.\]

And the gradient at $(x,y) =(-4,2)$ is equal to \[{dy\over dx} = {12 - 8 \over -24} = - {1\over 6}.\] As the tangents have the same gradient, the normal lines at these points will also have the same gradient, as the normal has the negative reciprocal gradient as the tangent, i.e. $m= 6$ for both normals.
The equations of the normals are $y = 6x+c$, where $c$ is the $y$-intercept. The normal to the point $(x,y) = (4,-2)$ needs to have $c = y-6x = -2 - 6\cdot 4 = -26$. The normal to the point $(x,y) = (-4,2)$ needs to have $c = 2+6\cdot 4 = 26$. So the distance between the $y$-intercepts is $52

Find the stationary points and determine their nature* for the curve with equation $y^2 = 3x^2 -2xy + 3$

*are they maxima, minima or indeterminate.

To find stationary points, we need to find the points where ${dy\over dx}=0$. So we take the $x$-derivative of the equation to get: \[ 2y{dy\over dx} = 6x -2y -2x{dy\over dx}. \] Which when rearranged gives: \[ {dy\over dx} = \frac{3x-y}{y+x}. \] This equals zero when $3x-y=0$ and $y+x\neq 0$. So when $y=3x$. We need to then find solutions to $y=3x$ and $y^2 = 3x^2-2xy+3$, which we can do by substituting $y=3x$ in the original equation: \[\begin{align} (3x)^2 &= 3x^2 - 2x(3x) + 3\\ 9x^2&= 3x^3 - 6x^3 +3\\ 12x^2 &= 3\\ x^2 &= {1\over 4}\\ x &= \pm {1\over 2}. \end{align} \] So we have that the stationary points are given by \[ (x,y) = (+{1\over 2}, +{3\over 2}),\ (-\frac{1}{2},-{3\over 2}). \]
To determine whether these stationary points are maximums or miminums (or indeterminates). We need to do the second-derivative test. We need an expression for ${d^2y \over dx^2}$, which we can get by taking the derivative of the expression for ${dy\over dx}$ using the quotient rule: \[\begin{align} {d^2y\over dx^2} &= \frac{(3-{dy\over dx})(y+x) - (3x-y)(1+{dy\over dx})}{(y+x)^2} \\ &= \frac{3y-3x -3x+y - {dy\over dx}(y+x -3x+y)}{(y+x)^2}\\ &= \frac{4y-6x - {dy\over dx}(2y-2x)}{(y+x)^2}. \end{align} \] Note that the points we are interested in have the property that ${dy\over dx}=0$. So we do not need to simplify this any further. For the point $(x,y) = ({1\over 2},{3\over 2})$ we have that: \[\begin{align} {d^2y\over dx^2} &= \frac{ \frac{12}{2}- \frac{6}{2} }{({3\over 2}+{1\over 2})^2} = \frac{6-4}{2^2}\\ &= \frac{2}{4} =\frac{1}{2}> 0. \end{align} \] Meaning that the stationary point at $({1\over 2},{3\over 2})$ is a minimum. For the point $(x,y) = (-{1\over 2},-{3\over 2})$ we have that: \[\begin{align} {d^2y\over dx^2} = \frac{-6 + 4}{(-2)^2} = \frac{-2}{4} <0. \end{align} \] Making this stationary point a maximum.

Show that \[ {d\over dx}a^{x^{k}} = k a^{x^k} x^{k-1}\ln(a) \]

Rewrite the expression as $a^{x^k} = (e^{\ln(a)})^{^{x^k}} = e^{\ln(a)x^k}$. Now if we take the derivative we can use the fact that ${d\over dx}e^u = e^u{dx\over du}$.

\[\begin{align} {d\over dx}(a^{x^k}) &= {d\over dx}(e^{\ln(a)x^k}) = e^{\ln(x)x^k} {d\over dx}(\ln(a)x^k) \\ &= e^{\ln(a)x^k}\ln(a) kx^{k-1} \end{align} \] Notice that $a^{x^k} = e^{\ln(a)x^k}$, so we have the answer.